LA CORRELAZIONE TRA LE VARIABILI DEL DATASET
Per capire meglio le correlazioni tra le variabili del dataset possiamo utilizzare l’indice di correlazione R per ranghi di Spearman mostrato nell’immagine seguente:
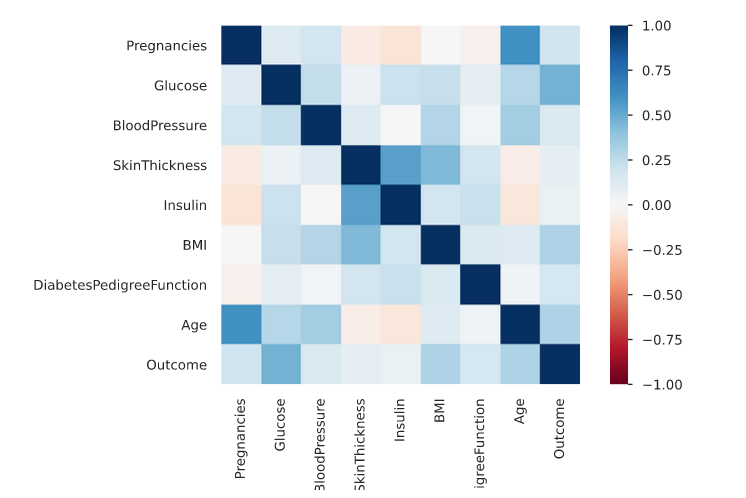
(Indice di correlazione R dei ranghi di Spearman)
Leggendo il grafico possiamo capire quanto le caratteristiche del dataset possano essere correlate tra loro. Leggendo il grafico presente in figura 10, vediamo, come la variabile “Age” risulta mediamente correlata con il numero di volte che la paziente è rimasta incinta (Pregnancies). Questa osservazione è desunta da un colore azzurro – scuro della scala presente a destra del grafico. Inoltre, si vede come la caratteristica “Age” sia mediamente correlata con la variabile “Outcome” e quindi con la presenza del diabete. Questo significa, che l’età, nell’ambito dei dati osservati, è mediamente correlata con la presenza del diabete. Tale osservazione era già stata estrapolata in un grafico a violino precedente. Allo stesso modo, possiamo vedere come la concentrazione di Glucosio “Glucose” sia mediamente correlata con la presenza del diabete. Nel grafico, tale correlazione è rappresentata con un colore tendente all’azzurro scuro della scala presente a destra del grafico. Ovviamente, queste considerazioni valgono su questo dataset di dati osservati appartenti alla popolazione dei Pima Indians.
Avendo caricato la libreria Scipy e la classe pearson possiamo verificare numericamente il coefficiente di pearson con l’aiuto del seguente codice.
18 correl = dataset.corr()
19 print(correl)
Il risultato delle righe 18 e 19 è il seguente:

(Coefficiente di correlazione tra le variabili del dataset).
Come indicato, dai risultati presenti nella figura 11, vi è una correlazione maggiore tra le variabili concentrazione di Glucose, Age, BMI, Pregnancies e la variabile Y Outcome. Risultano interessanti anche altre correlazioni e in particolare quella tra Age e Pregnancies o Insulin e Skin tickness. La correlazione più alta è quella relativa alla variabile Age e la variabile Pregnancies uguale a 0,544 ma comunque minore di 0,70 dove si avrebbe, in tal caso, una situazione di multicollinearità.
Ma cosa significa multicollinearità?
Facciamo un breve esempio. Consideriamo le variabili X1 e X2 rispettivamente indicanti la prima, il reddito lordo e la seconda il reddito netto. Y rappresenta la nostra variabile di spesa o meglio il nostro output. X1 e X2 sono fortemente correlate e il calcolo della regressione di Y su X1 e X2 darebbe dei dati non significativi.
Un commento su “Il modello sequenziale di Keras: un esempio di utilizzo.”
Utile