37 model.compile(loss='mse', optimizer='rmsprop')Continuando con la spiegazione del codice, nella riga trentasette (che ho riportato sopra), al metodo compile vengono passati due parametri: il primo, la funzione di costo e il secondo l’ottimizzatore. Per quanto concerne la funzione di costo, in questo caso abbiamo utilizzato il valore MSE, ossia lo scarto quadratico medio definito dalla seguente formula:
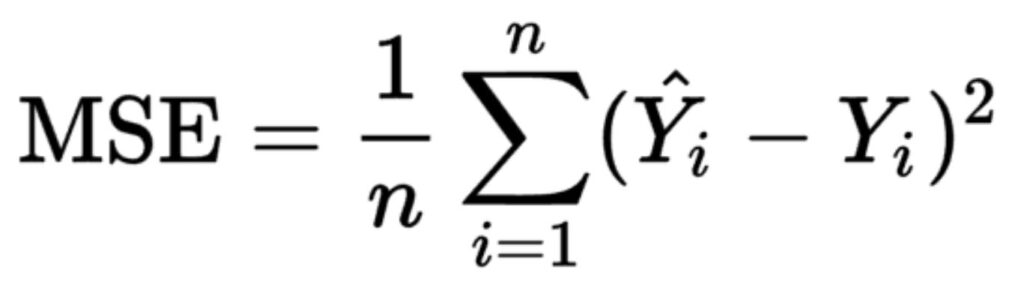
(Mse come funzione di costo della nostra rete neurale)
In sostanza, più il valore di MSE è tendente a zero e più la nostra rete neurale “approssima” il valore calcolato al valore reale. Quando la funzione di costo e quindi MSE è uguale a zero, significa che il valore calcolato (o predetto) è uguale al valore reale. La ricerca della differenza minima tra questi due valori diventa essenziale, e la standardizzazione adottata nei valori in input aiuta a far convergere più velocemente la funzione di costo verso il valore di differenza minima. Avete certamente capito, che il valore predetto risulta migliore o più preciso quando il valore della funzione di costo è uguale a 0. Con i processi di “forward propagation” che abbiamo visto e di “backward propagation” (che vedremo) la rete neurale nella fase di training, “ricerca” i pesi per i quali l’output risulta uguale al valore reale calcolando tale differenza con la funzione di costo, che in questo caso è espressa dal valore MSE.
Per il momento, anche se non è tutto chiaro, è utile sapere quanto riassunto nei seguenti punti:
1) La rete neurale è composta da più livelli, un livello di input, uno o più livelli intermedi e un livello finale o di output.
2) Le informazioni vengono trasmesse dal livello di input al livello di output e vengono elaborate secondo dei pesi e dalle funzioni di attivazione.
La riga trentasette come abbiamo già detto definisce con il metodo compile della classe Sequential la funzione di costo, di cui abbiamo già parlato, e imposta come ottimizzatore l’algoritmo “rmsprop”. L’ottimizzatore “rmsprop” serve a far confluire più rapidamente la funzione di costo (MSE) al valore minimo come evidenziato nella figura seguente per ricavarne un valore sempre più vicino al valore reale.
(L’ottimizzatore RMSPROP.
Source: https://imgur.com/a/Hqolp#NKsFHJb).
Concludo questa parte di appunti, in cui abbiamo visto un bel po’ di codice sperando di avervi incuriosito abbastanza. Nella prossima parte, cercheremo di completare questo esercizio calcolando la previsione di un prezzo futuro di un asset con l’aiuto della rete neurale che abbiamo fin qui costruito.
Link alle parti precedenti degli appunti di Machine Learning:
Appunti di Machine Learning in ambito finanziario I parte.
Appunti di Machine Learning in ambito finanziario II parte.
Appunti di Machine Learning in ambito finanziario III parte.
Come al solito, per eventuali domande e integrazioni inviate un e-mail a webmaster@megalinux.cloud. Aiutate a sostenere The Megalinux, l’unico sito nel Web senza pubblicità inviando Bitcoin al seguente indirizzo.
3LpoukFpvDHTZPn5qGbLwUzve3rX9zsSq6
