Un secondo esempio del processo di “forward propagation”.
Ecco un secondo esempio di propagazione dai valori di input ai valori di output della rete neurale.
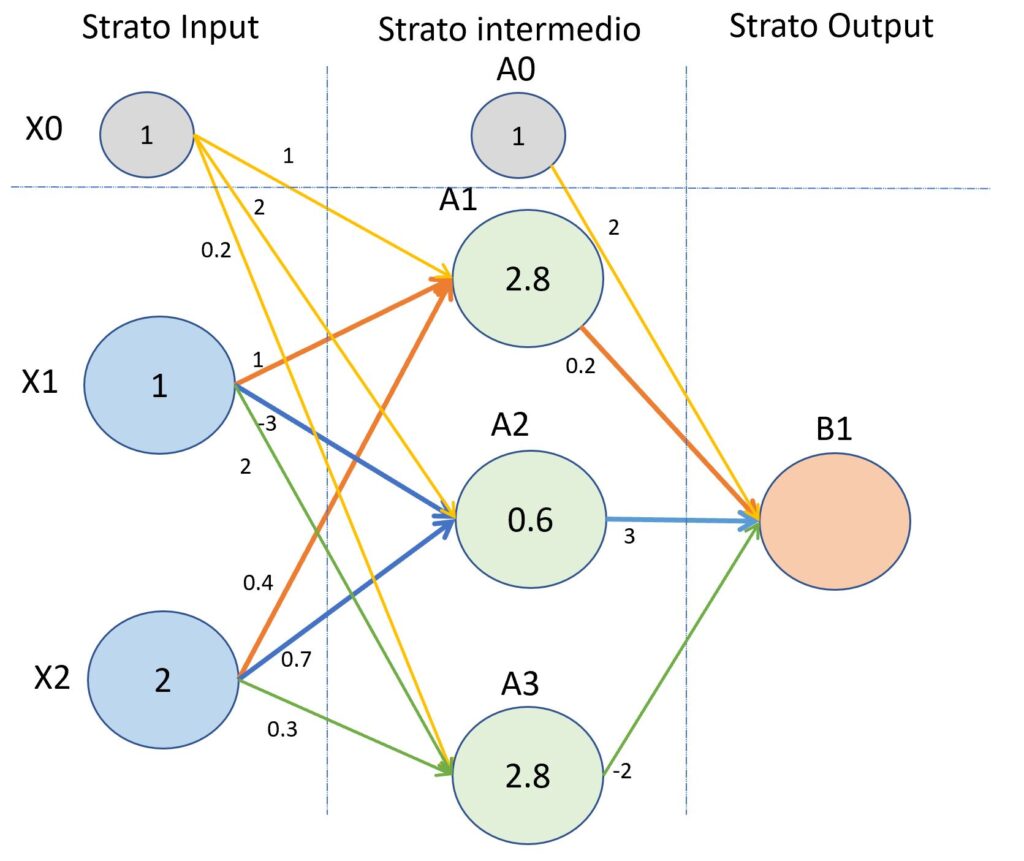
(Secondo esempio del processo di “forward propagation”)
Come per il primo esempio, partiamo dal determinare il valore in ingresso del nodo A1.
ValA1 = (X1 x w(1)11)+(X2 x w(1)12) + (X0 x w(1)10)
ValA1 = (1 x 1+2 x 0.4)+1 x 1
ValA1 = (1+0.8)+1 = 2.8
Il valore in ingresso del nodo A2 si determina nel seguente modo.
ValA2 = (X1 x w(1)21)+(X2 x w(1)22)+ (X0 x w(1)20)
ValA2 = (1 x -3+2 x 0.7)+1 x 2
ValA2 = -1.6+2 = 0.6
Il valore in ingresso del nodo A3 si determina nel seguente modo.
ValA3 = (X1 x w(1)31)+(X2 x w(1)32)+ (X0 x w(1)30)
ValA3 = (1 x 2+2 x 0.3)+1 x 0.2
ValA3 = 2.6 +0.2 = 2.8
Applicando la funzione di attivazione “Relu” al valore del nodo A1, F(2.8),al valore del nodo A2, F(0.6), e infine al valore del nodo A3, F(2.8), i valori in uscita dai nodi saranno rispettivamente 2.8,0.6,2.8 come mostrato nell’immagine successiva. Abbiamo già parlato di come funziona la funzione di attivazione.
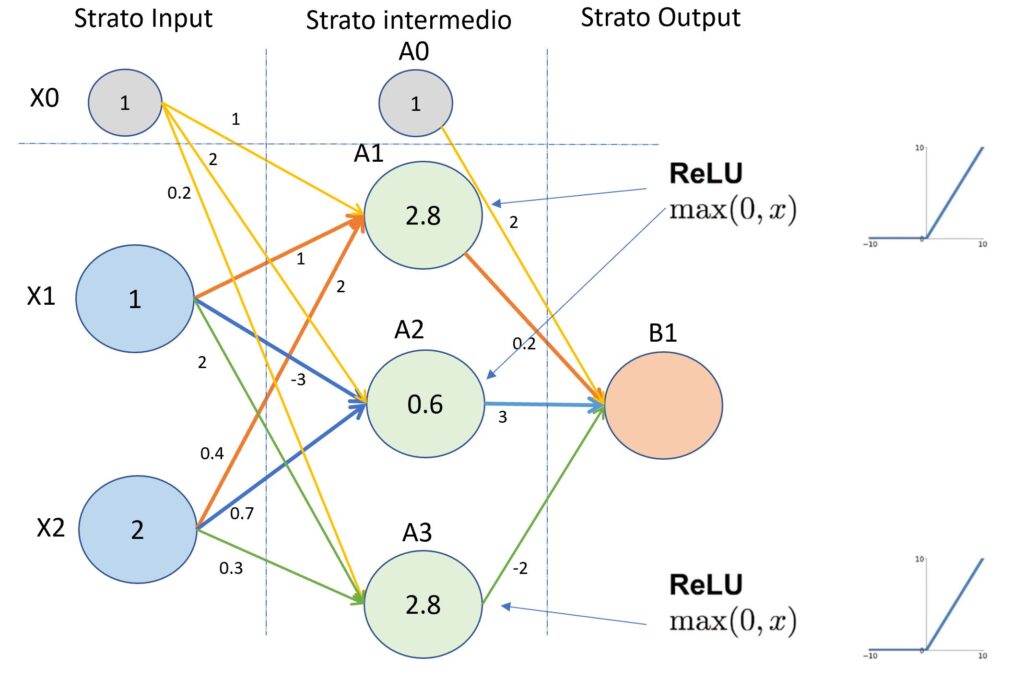
(Secondo esempio del processo di “forward propagation”)
A questo punto, calcoliamo i valori del nodo B1.
ValB1 = (A1 x w(2)11)+(A2 x w(2)12)+ (A3 x w(2)13)(A0 x w(2)10)
ValB1 = 2.8 x 0.2 + 0.6 x 3 +2.8 x -2 = 0.56 + 1.8-5.6 = -3.24
Applicando la funzione Lineare al valore -3.24 e cioè ValB1 l’output finale della rete neurale è uguale a -3.24. Di seguito l’immagine con evidenziato il valore del nodo di output della rete neurale di esempio.
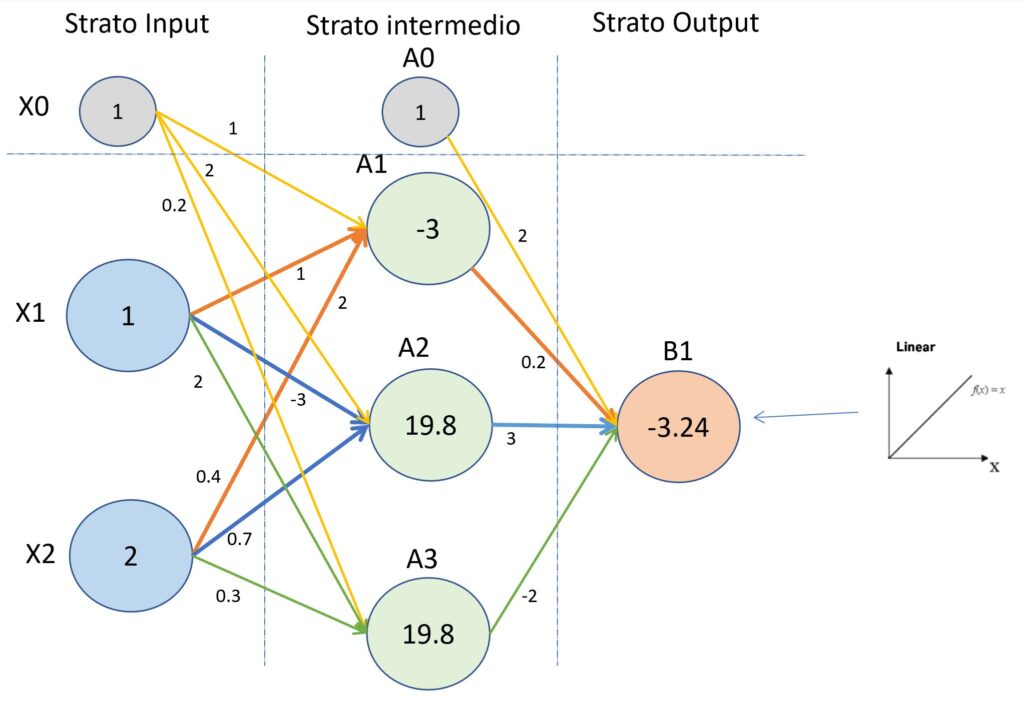
(Secondo esempio del processo di “forward propagation”)