Ora, per ognuno dei valori ValA1 e ValA1 si applica la funzione di attivazione o di trasferimento. Come nel caso in oggetto di studio, la funzione di attivazione è la “Relu”, e per tale, possiamo aggiungere le seguenti osservazioni. Quando l’input è negativo, questo verrà convertito in un valore zero e il neurone non si attiverà. Questo significa che verranno attivati solo pochi neuroni rendendo la rete più efficiente e facile per il calcolo. Quando l’input è positivo si lascerà il valore invariato.
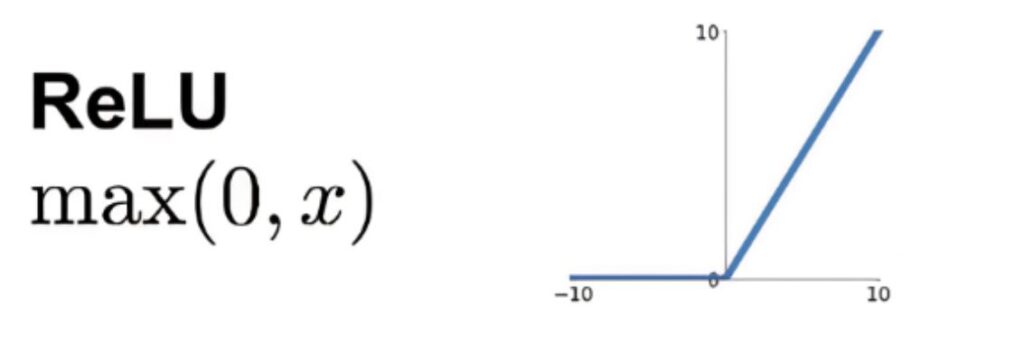
(La funzione di attivazione “ReLu”).
Tornando ai valori dello strato intermedio ValA1 e ValA2, e applicando la funzione di attivazione “Relu” al valore del nodo A1 F(-3) e al valore del nodo A2 F(19.8), i valori saranno rispettivamente 0 e 19.8 come mostrato nell’immagine successiva.
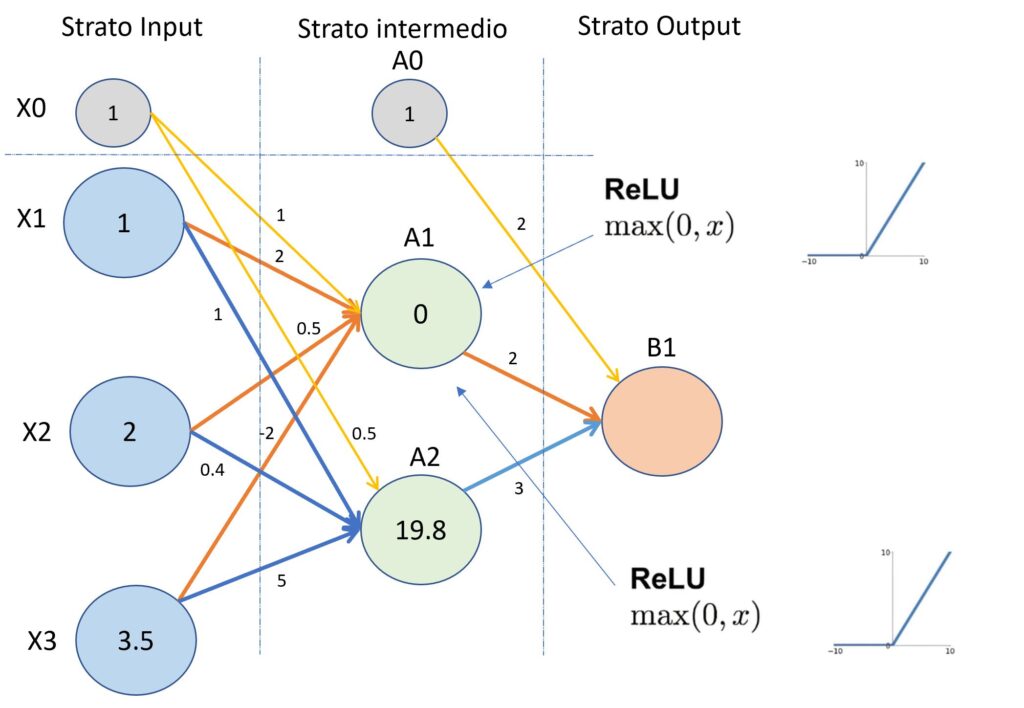
(Primo esempio del processo di “forward propagation”).
A questo punto, per calcolare il valore di output del nodo di uscita B1 dobbiamo procedere come di seguito descritto. Nel calcolo ValB1 ho escluso il calcolo del nodo A1 in quanto è un neurone non attivato e di conseguenza non trasmetterà nulla al nodo B1.
ValB1 = A2 x w(2)12 +A0 x w(2)10
ValB1 = 19.8 x 3 + 1 x 2 = 61.4
B1 = F(ValB1) = 61.4 (applicazione della funzione lineare al valore ValB1.
L’immagine seguente vi mostra al nodo B1 il valore calcolato.
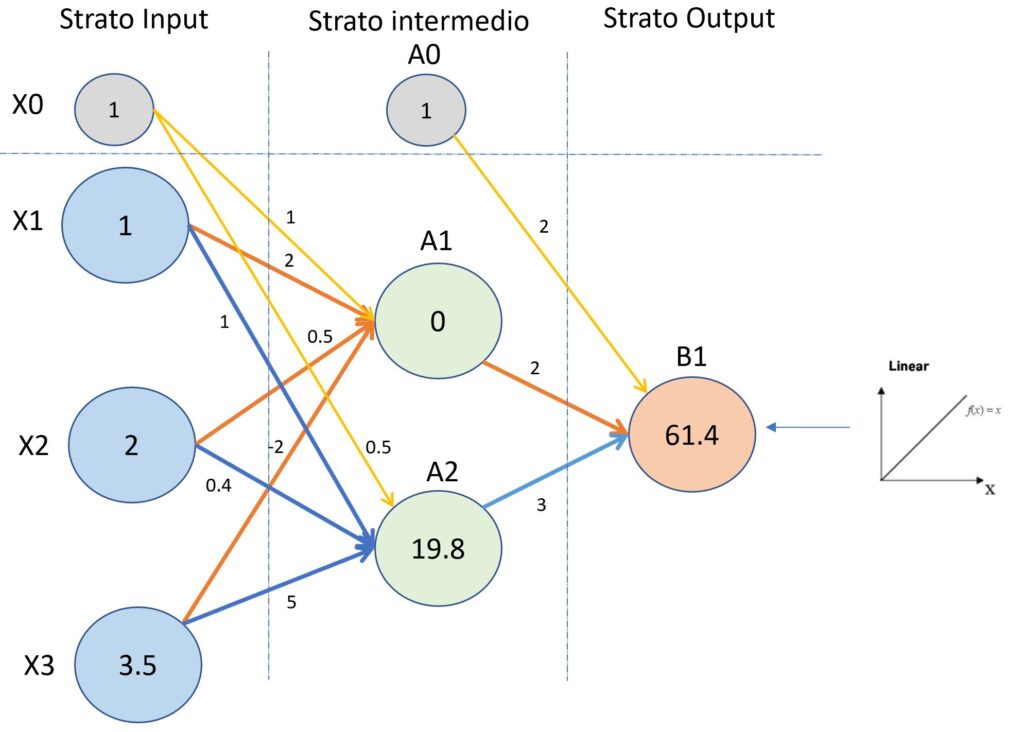
(Primo esempio del processo di “forward propagation”).
Infine, applicando la funzione di attivazione “Linear” al valore del nodo B1 il valore rimarrà invariato. Se invece applicassimo un altro tipo di funzione di attivazione il valore di uscita potrebbe cambiare in ragione della funzione applicata.