Dato, che stiamo utilizzando per il progetto un tipo di modello di rete neurale sequenziale, nelle righe trentacinque, trentasei e trentasette definiamo i vari livelli. In particolare, nella riga trentacinque aggiungiamo il livello di input passandogli un numero di parametri definito dalla variabile “total_columns” e un livello nascosto (hidden) di tipo Dense con 512 neuroni e funzione di attivazione ‘Relu’.
Nella riga trentasei aggiungiamo infine il livello di output di tipo Dense con un neurone e funzione di attivazione ‘Linear’.
In pratica, il primo layer, quello di input è differente dai successivi perché non riceve alcuna informazione da nessun layer precedente. Di fatto, tale livello, rappresenta lo stato iniziale della rete neurale. Nello strato intermedio o nascosto i dati vengono rielaborati in base ai pesi e alle funzioni di attivazione, e passati, all’ultimo layer, quello di output, che come risultato finale restituisce il prezzo della pair considerata.
Possiamo immaginare la nostra rete neurale come una scatola nera, ove vi sono degli input e degli output. Dentro alla scatola non sappiamo cosa accade, ma per iniziare, possiamo dire che all’interno della nostra scatola sono presenti degli strati o livelli intermedi nascosti.
L’unità principale è il neurone e ogni strato ne contiene da uno a N. Normalmente, ogni neurone è collegato a tutti i neuroni dello strato successivo attraverso delle connessioni pesate, in cui, il peso, è un valore numerico che viene moltiplicato per il valore del neurone collegato. Ogni neurone, somma i valori di tutte le “sue” connessioni pesate, aggiunge un valore di “bias”, e a questo risultato viene applicata una funzione di attivazione che trasforma matematicamente il valore prima di passarlo allo strato successivo. Se l’output di tale funzione, supera una determinata soglia, tale output attiva il nodo, passando i dati al livello successivo della rete. Per tale motivo, tale funzione, viene anche detta di trasferimento, e si applica ai layer nascosti (hidden) e non ai layer di input o di output. Questo processo di passaggio dei dati da un livello a quello successivo è chiamata tecnicamente “forward propagation”.
E’ fondamentale capire che per raggiungere il risultato voluto, pesi e bias si regolano in modo automatico durante il processo di training di una rete neurale. Il come i pesi si regolano durante la fase di training è un argomento che merita una trattazione a parte più approfondita.
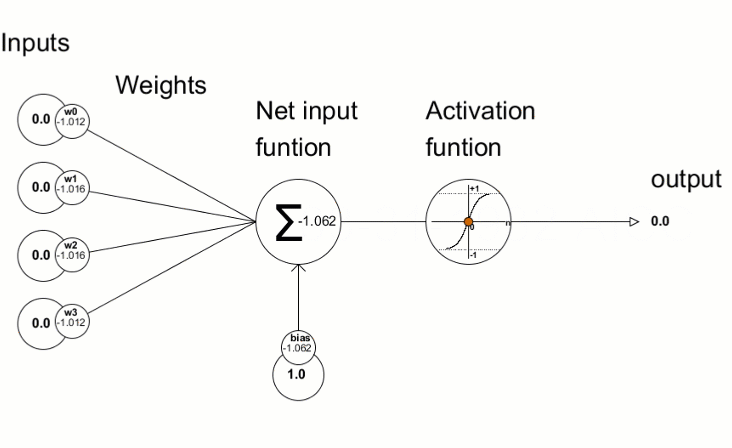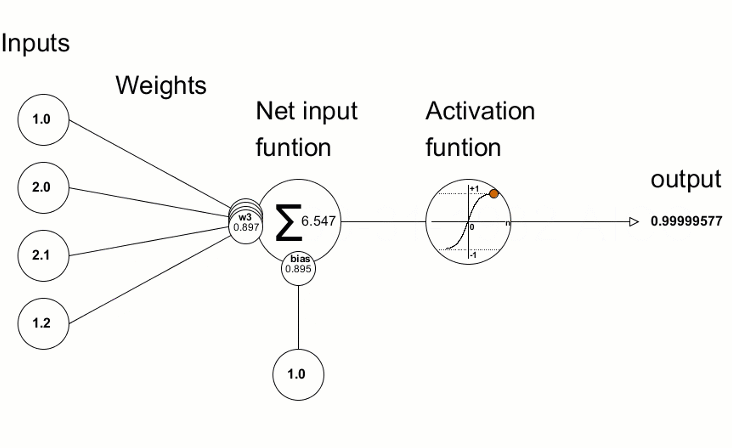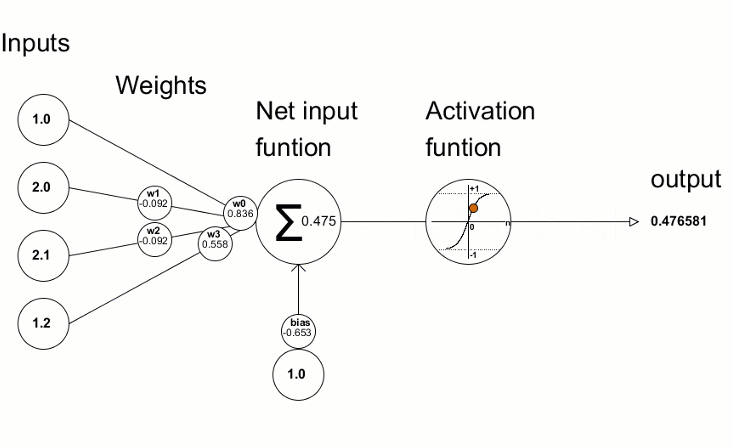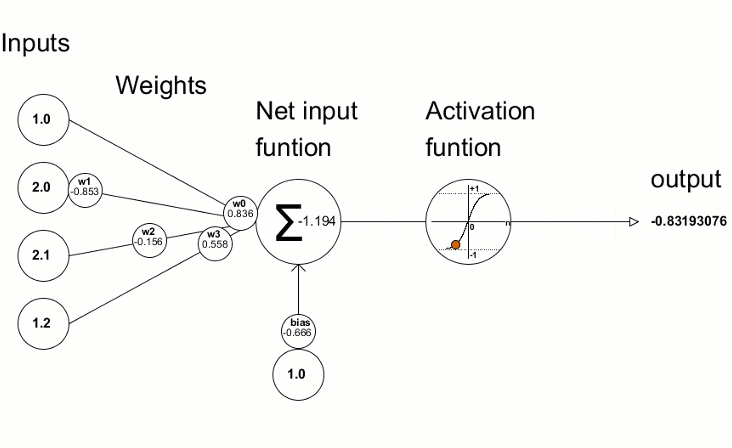
(Trasmissione delle informazioni all’interno di un neurone:
Source: Programming a Deep Neural Network from Scratch using MQL Language – Articoli MQL5).
Per comprendere al meglio il funzionamento di una rete neurale, ho ritenuto opportuno fare un esempio concreto descrivendo il processo di “forward propagation”.
Un primo esempio del processo di “forward propagation”.
La seguente immagine mostra una rete neurale composta da tre strati, quello di input, uno intermedio e uno finale di output.
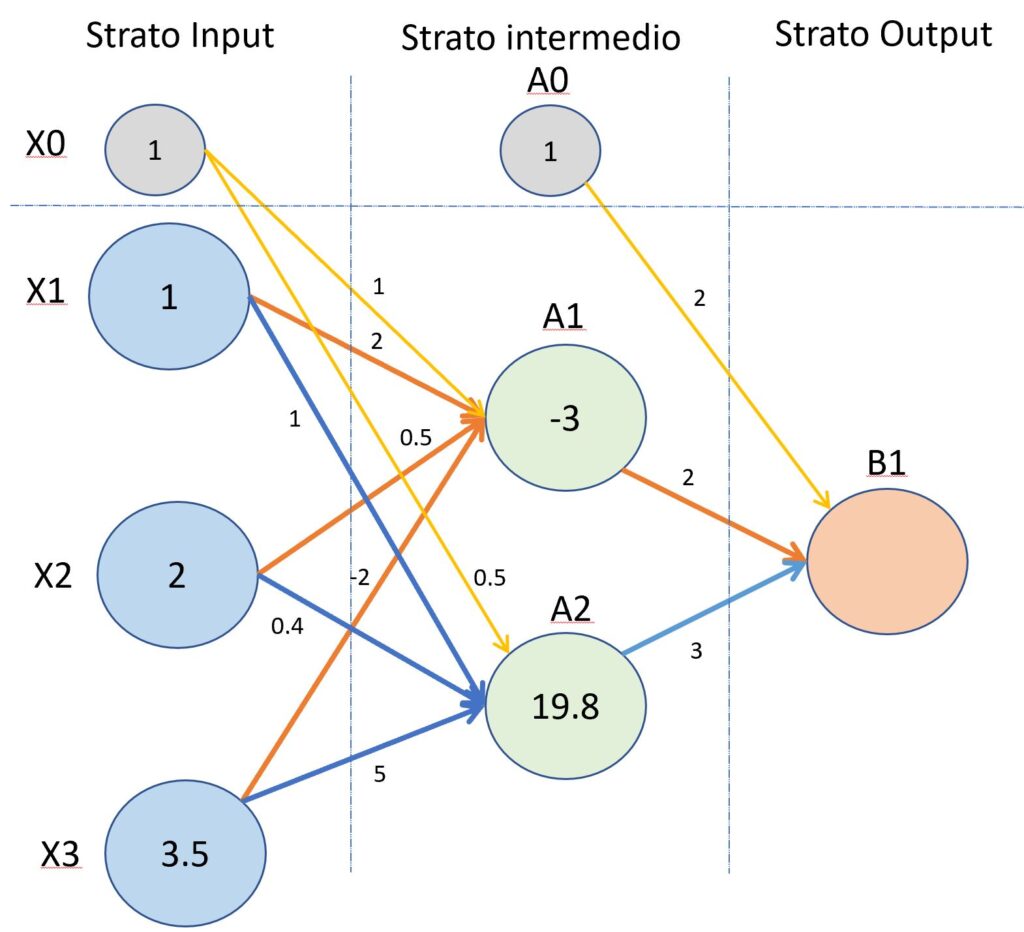
(Primo esempio del processo di “forward propagation”).
Ora, proviamo a calcolare i valori che vengono trasferiti attraverso gli strati della rete neurale facendo riferimento alla figura tre. I nodi del secondo strato (quello nascosto), avranno come ingresso la somma dei nodi X1,X2,X3 “pesati” dalle connessioni. Il valore ricevuto dal nodo A1 sarà uguale al seguente calcolo.
ValA1 = (X1 x w(1)11)+(X2 x w(1)12)+(X3 x w(1)13) + (X0 x w(1)10)
ValA1 = (1 x 2+2 x 0.5+-2 x 3.5)+1 x 1
ValA1 = (2+1-7)+1 = -3
Il valore ricevuto dal nodo A2 sarà calcolato come di seguito mostrato.
ValA2 = (X1 x w(1)21)+(X2 x w(1)22)+(X3 x w(1)23) + (X0 x w(1)20)
ValA2 = (1 x 1+2 x 0.4+3.5 x 5)+1 x 0.5
ValA2 = 19.3 +0.5 = 19.8
Nota: il primo indice presente nel pedice, dopo il peso indicato dalla lettera w, si riferisce ai neuroni del livello di intermedio, mentre il secondo indice fa riferimento al neurone del layer precedente ossia, in questo caso il layer di input. L’indice presente all’apice rappresenta il numero di layer: 1 per il layer di input, 2 per il layer nascosto e così via.
Come si vede, nel calcolo vengono introdotti dei neuroni di bias che permettono di modificare il risultato dei valore trasmesso, così da ottenere una maggiore variabilità e quindi la possibilità di ottenere un risultato più vicino al valore reale.
Per capire più semplicemente la funzione del neurone di bias possiamo dire che ha la stessa funzione della costante b nella seguente funzione lineare:
y = ax + b
Con la costante b la linea può muoversi dall’origine, invece, senza la costante b la funzione lineare è “ancorata” all’origine.