In questa terza parte, utilizzeremo il modello della regressione polinomiale per trovare la funzione che meglio approssima i valori reali dell’andamento di una pair con l’obiettivo di poter “calcolare” il valore futuro del prezzo dell’asset. Inoltre, vedremo come misurare l’approssimazione dei valori predetti (calcolati con l’equazione desunta della regressione lineare) e i valori reali con l’aiuto dell’indice MSE ossia il mean squared error (errore quadratico medio).
Inizieremo a studiare il codice Python dal punto in cui avevamo concluso con la seconda parte e quindi, con le righe seguenti.
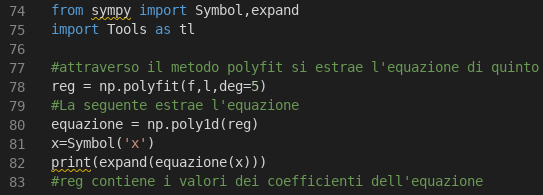
(Metodo polyfit ed estrazione dell’equazione che meglio approssima i valori reali).
La riga settantotto applica il metodo polyfit per trovare i coefficienti della funzione di quinto grado (deg=5) che meglio approssimano i vettori (ndarray) f, ed l. Quest’ultimi, sono rispettivamente i valori del tempo (data del prezzo) e i valori del prezzo dell’asset ETH rispetto alla currency BTC. I coefficienti vengono “salvati” nel vettore reg (v. immagine successiva).

(Valori dei coefficiente dell’equazione di quinto grado).
Le righe ottanta, ottantuno, ottantadue estraggono la funzione di quinto grado, con l’uso del metodo poly1d della classe Numpy, e la stampano a video. Per far ciò, sono state importate alcune classi della libreria Simpy nella riga settantaquattro e più precisamente la classe Symbol ed expand. Di seguito, un esempio di equazione di quinto grado espressa in notazione scientifica.
4.69631986339609e-6 x5 + 1.9422135509022e-5 x4 + 8.66365575948904e-5 x3 – 0.00015111931200399 x2 – 0.000224280612004323 x + 0.000140868989531326
Nella riga settantacinque ho importato la classe Tools. Quest’ultima è una classe che contiene il metodo MSE per il calcolo dell’errore quadratico medio e quindi la misura dell’approssimazione della funzione trovata attraverso l’uso della regressione polinomiale. Ecco, le righe del metodo MSE della classe Tools.

(Metodo MSE per il calcolo dell’errore quadratico medio della classe Tools).
Come potete vedere al metodo vengono passati fondamentalmente due parametri (il primo “self” dice al metodo che appartiene alla classe Tools), il vettore l, che in questo caso sono i valori reali e il vettore p, che non sono altro che i valori predetti dalla funzione precedente di quinto grado. Più il valore MSE è piccolo, più la funzione approssima i valori reali. La formula dell’errore quadratico medio (MSE) risulta descritta nella seguente immagine.

(Formula dell’errore quadratico medio)
Per capire, se la funzione di quinto grado meglio approssima i dati reali dobbiamo calcolare il valore dell’errore quadratico medio. Come già detto, più questo valore tende a 0, e più i valori predetti sono approssimati ai valori reali.
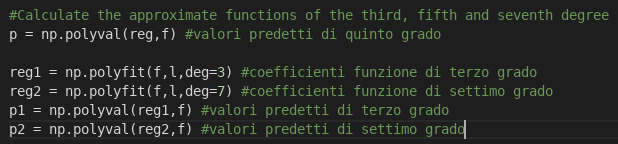
(Calcolo dei valori stimati)
Questa parte di codice risulta molto importante, perché è tra queste righe che si calcolano i valori stimati dalle funzioni di terzo, quinto e settimo grado. Nella riga 84 si applica il metodo polyval della classe Numpy per calcolare i valori stimati passando i coefficienti della funzione di quinto grado (reg), e i valori del vettore f (asse x dell’andamento delle pair). Il vettore p (ndarray) conterrà i valori stimati. La riga ottantacinque e la riga ottantasei salvano nei vettori reg1 e reg2 rispettivamente i coefficienti della funzione di terzo e di settimo grado. La righe 87 e 88 salvano nei vettori p1 e p2 i valori stimati della funzione di terzo e settimo grado.

(Calcolo e stampa dell’errore quadratico medio).
Nella riga novanta l’oggetto tl1 istanzia la classe Tools. Nelle successive, novantuno, novantadue e novantatré vengono stampanti i valori dell’errore quadratico medio di cui abbiamo già ampiamente parlato, passando il vettore l dei valori reali e il vettore pi dei valori stimati. A questo punto, non ci resta che rappresentare con un grafico le varie funzioni di terzo, quinto e settimo grado e i valori reali. Le seguenti righe di codice servono a questo scopo.
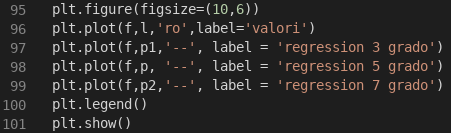
(Visualizzazione con Matplotlib delle funzioni di terzo, quinto e settimo grado).
Come potete vedere, la riga novantasei disegna i punti ‘ro’ dei vettori f ed l. Questi rappresentano i valori reali. Le successive righe, la novantasette, la novantotto e la novantanove disegnano le funzioni ‘–‘ dei vettori f, pi
La riga 101 visualizza il grafico con il metodo show della classe Matplotlib.
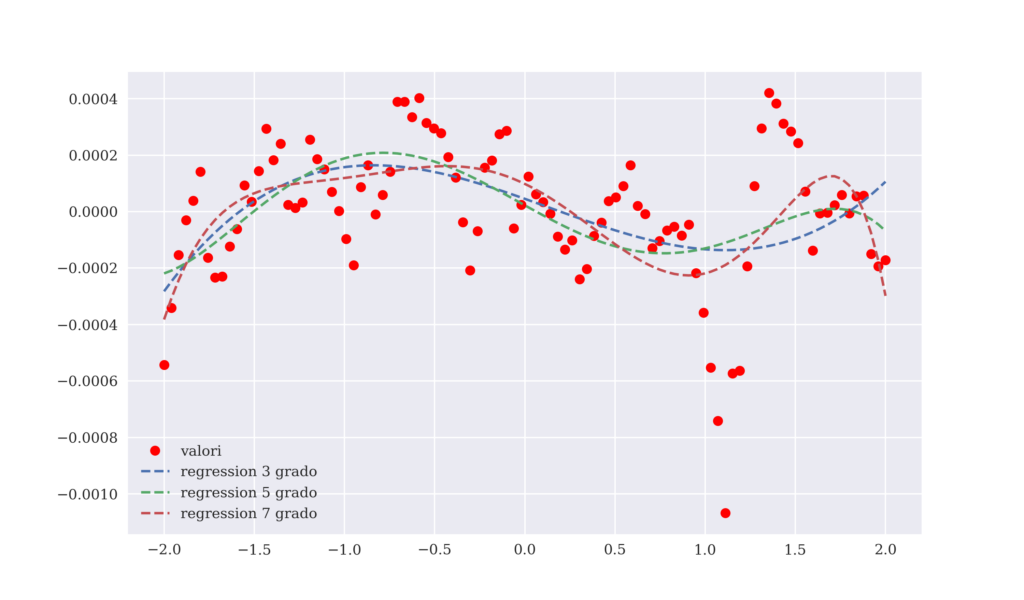
(Visualizzazione delle funzioni di approssimazione calcolate con il metodo della regressione polinomiale).
L’immagine otto risulta fondamentale allo scopo del nostro obiettivo. In questa si possono vedere rappresentati tutti i valori stimati dalle funzioni di terzo, quinto e settimo grado. In base al valore dell’errore quadratico medio la funzione di settimo grado meglio approssima i valori reali.